[コンプリート!] ピタゴラス の 定理 直角 三角形 255968-ベクトル 直交 完 備 ピタゴラス
ピタゴラスの定理の簡単な証明方法ありますか Quora
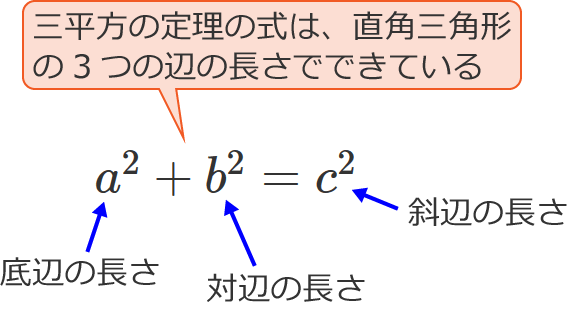
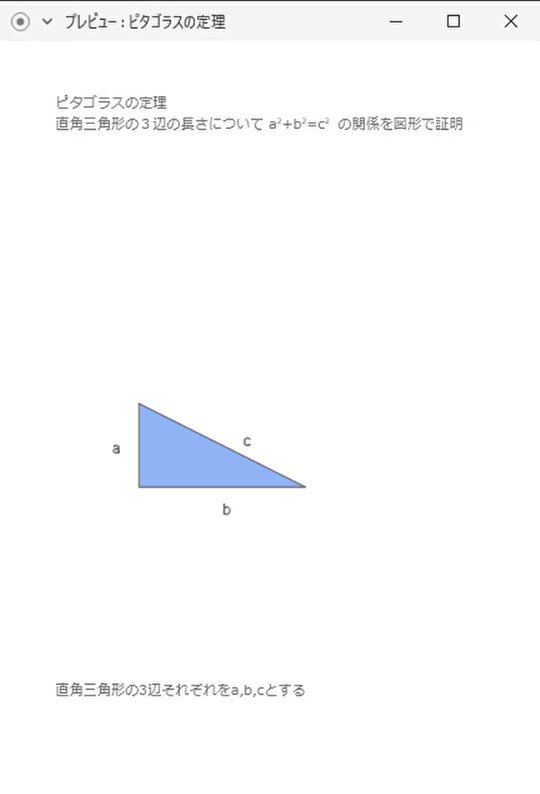
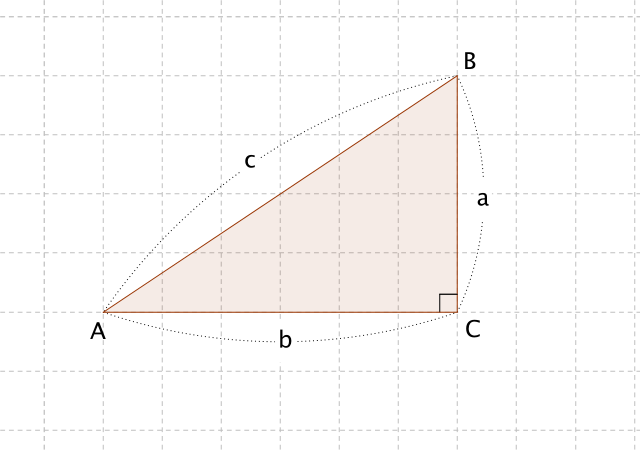
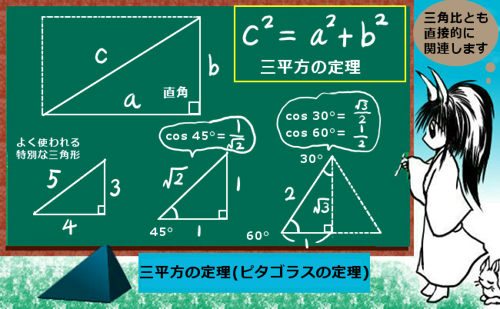
ピタゴラスの定理 (ピタゴラスのていり)は、 直角三角形 の3 辺 の長さの関係を表す 等式 である。 三平方の定理 (さんへいほうのていり)、 勾股弦の定理 (こうこげんのていり)とも呼ばれる。 3つの辺の比が : : になっていれば、必ず直角三角形になります。 諸説ありますが、古代エジプトではこの形を使って直角を計り、ピラミッドを作ったのではないか、と言われてい
ベクトル 直交 完備 ピタゴラス
ベクトル 直交 完備 ピタゴラス- ピタゴラスは遅かった 三平方の定理「最古の応用例」 畑の図面が記されている粘土板。 三平方の定理を使って面積や形が正確に描かれている 数学の課題でわからない分野があるのですがわかる方いたら教えていただきたいです。大至急です。 1三角形の内角の和を求めなさい。 2五角形の内角の和を求めなさい。 3十角形の
Many Proofs Of Pythagorean Theorem
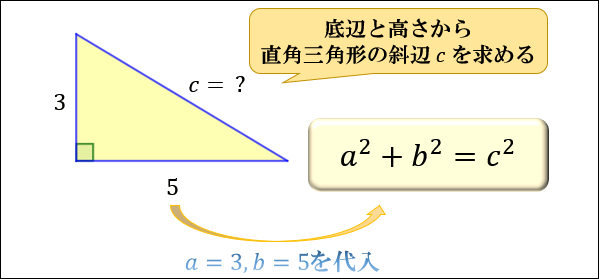
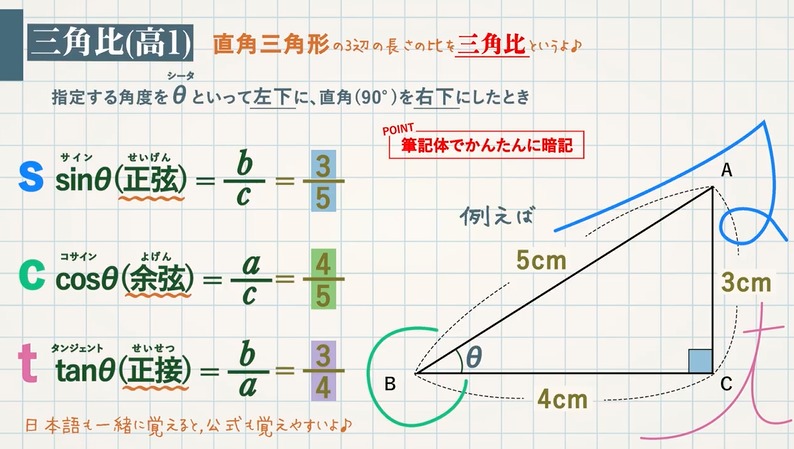
まず覚えておいておくべき直角三角形の辺の比は、 12√3 だよ。 この辺の比になる直角三角形の角度は、 30° 60° 90° になってるんだ。 例えば、次の直角三角形ABCがあったとして三平方の定理(ピタゴラスの定理) 三平方の定理 は、直角三角形の辺の長さを求めるときによく使われる定理で、数学の中でもとても重要な定理の一つです。 三平方の定理を初めて習ったのは中学レッグ(b)の結果: ピタゴラスの定理 直角三角形の場合:斜辺(c)の二乗値は、脚(a)の二乗値と脚(b)の二乗値の合計に等しくなります。 斜辺(c)の計算 レッグ(a)の計算 レッグ(b)
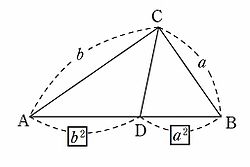
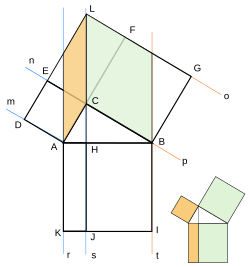
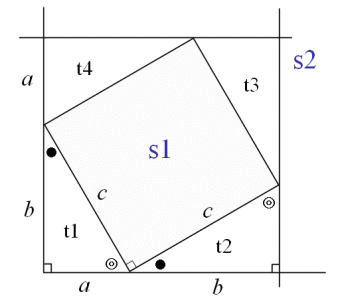
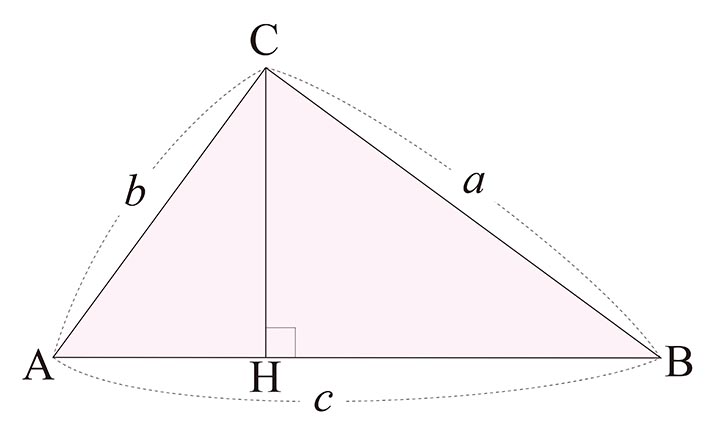
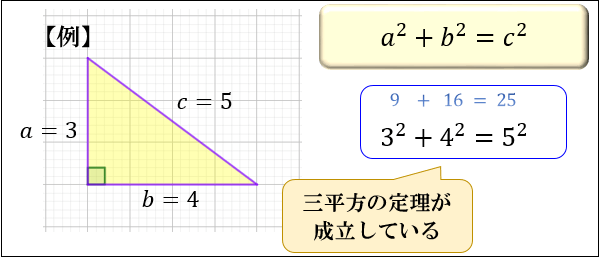
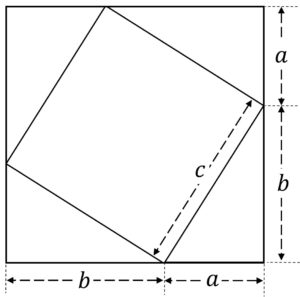
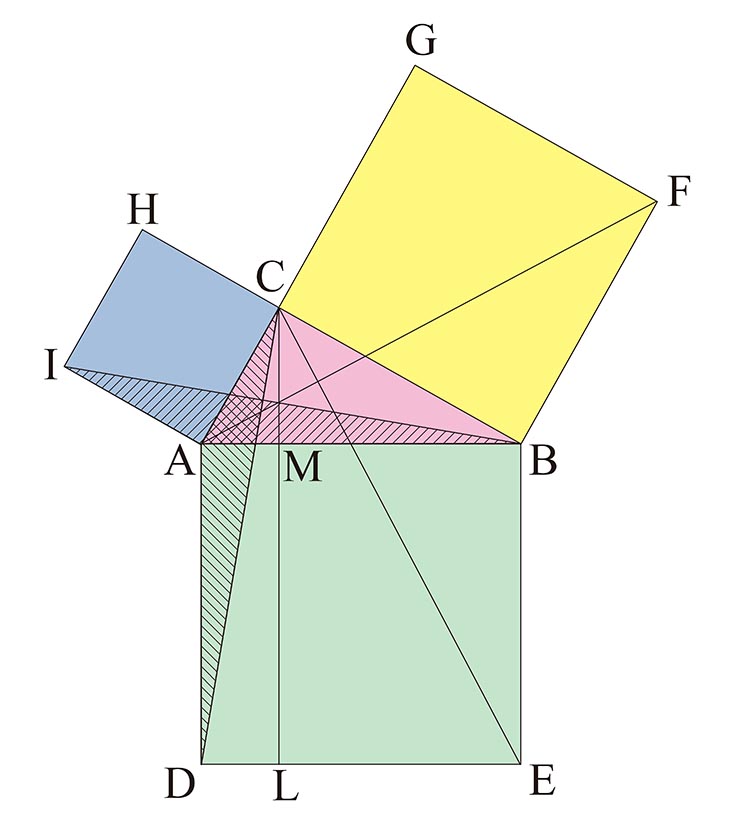
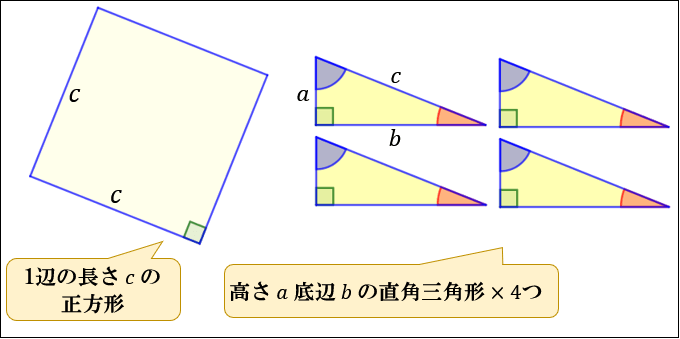
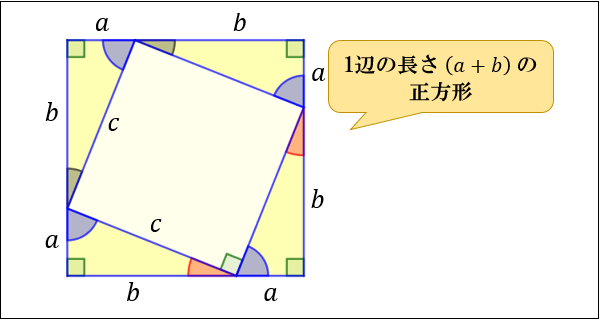
ピタゴラスの定理とは 上のような直角三角形があるときに が成り立つという定理である。 また、自然数である (a, b, c)の組をピタゴラス数という。 証明 大きい正方形の面積を、二通り 直角三角形において、「直角」をはさむ2つの辺の長さを \(a,b\)、斜辺の長さを \(c\) としたとき 三平方の定理(ピタゴラスの定理)と公式の証明忍者が用いた三角の知恵|アタリ ピタゴラスの定理の証明 この定理には数百通りもの異なる 証明 があり、例えば、「以下では頂点 A, B, C からなる三角形を ABC と表す」「各辺 AB, BC, CA に向かい合う角をそれぞれ
ベクトル 直交 完備 ピタゴラスのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
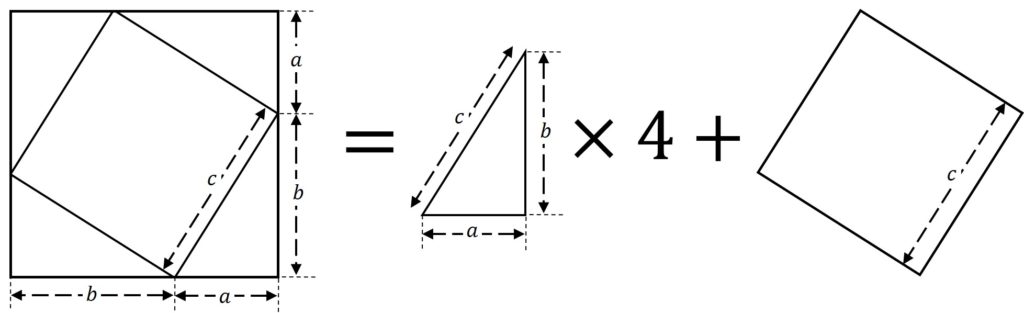 |  |  |
「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
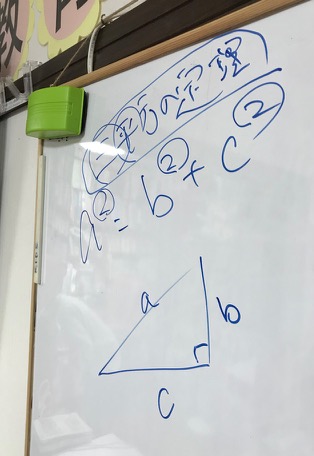 |  |  |
 |  |  |
「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。
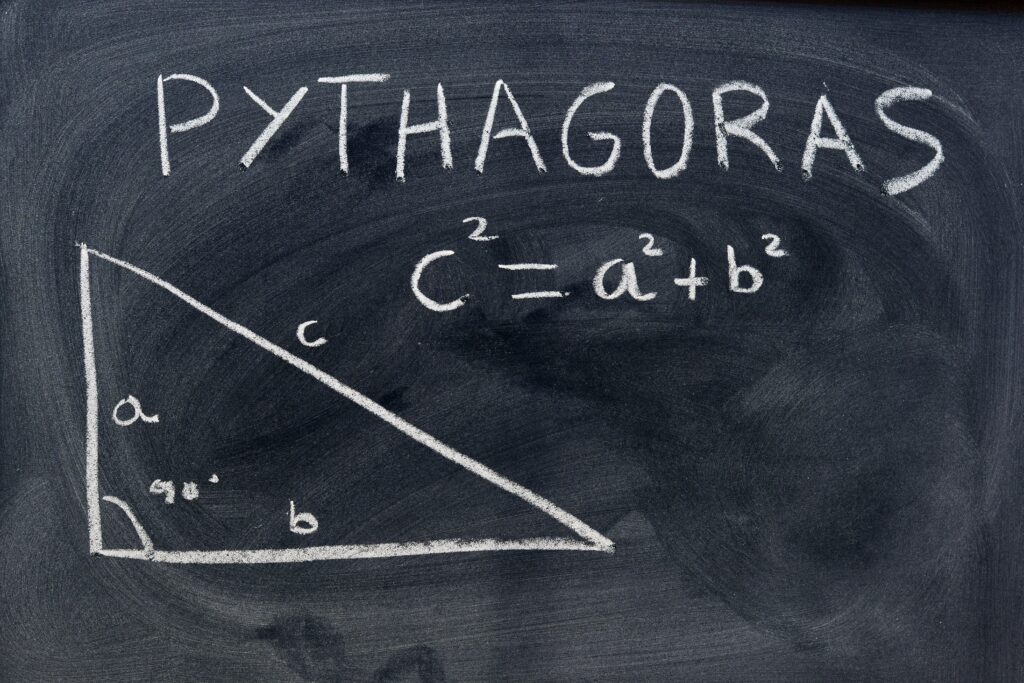 | ||
 | ||
 | 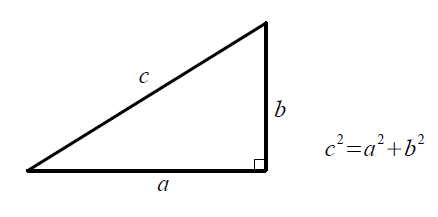 | |
「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「ベクトル 直交 完備 ピタゴラス」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
直角三角形(ちょっかくさんかくけい、英 right triangle )は、三角形の一種である。 三角形の3つの内角のうち、他のどの内角よりも小さくない角に注目したとき、その角が直角 (90°=π/2 rad) に直角三角形の3辺の長さに関する a 2 b 2 =c 2 という関係は ピタゴラスの定理 (三平方の定理)と呼ばれます。 この定理はその名の通り古くから知られていますが、本当にピタゴラス (cBC570
Incoming Term: ピタゴラスの定理 直角三角形, ピタゴラスの定理 1 2 ルート3, ベクトル 直交 完備 ピタゴラス,
コメント
コメントを投稿